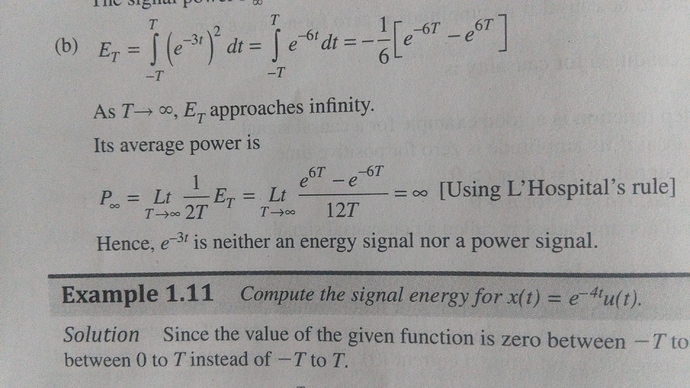Which of the following is the correct statement? The continuous time system described by \displaystyle{y}{\left({t}\right)}={x}{\left({t}^{2}\right)} is
a) causal, linear and time-varying
b) causal, nonlinear and time-varying
c) non-causal, nonlinear and time-invariant
d) non-causal and time-variant
Plz give the solution.
Ans d is the correct one
Option D is correct
sol - For causal - output depends only on the present value only, it should not take any future value.
But in this problem, if you put t=2, y(2) = x(4), means it depends upon the future instance of time. So, the given signal is non-causal.
Time Dependency -
If a system is having time scaling it would be time variant. This time scaling could be on both sides, input or output.
Please go through the videos for system property provided by Neso academy, they have explained it very well. After watching those videos you would hardly take 20 sec to answer these questions.
Sir i have a doubt you said that an infinite extension signal with decreasing amplitude will be an energy signal but in this case it is NENP signal , please explain it
Y(t-to)=x(t-to)^2
now taking x(t) and making shift by to then resulting answer will be x(t^2-to) and mark one thing that only variable t is being squared not whole term because to is a constant
but according to question only system makes square of variable so it is time variant
and for t=2 output depends on x(4) which is a future value of input so non causal
hope u have got your answer
What is the book hou are referring , please
Vimalkumar
option d is correct
y(2)=x(4)
present input depends on future output… it is non causal
power is non linear operator
delayed output y(t-to) x((t–to)^2)
for delayed input x(t-to) , the output y(t) is x(t^2-to)
therefore the system is time varient
